1028. Recover a Tree From Preorder Traversal.md

1028. Recover a Tree From Preorder Traversal

We run a preorder depth first search on the root of a binary tree.

At each node in this traversal, we output D dashes (where D is the depth of this node), then we output the value of this node. (If the depth of a node is D, the depth of its immediate child is D+1. The depth of the root node is 0.)

If a node has only one child, that child is guaranteed to be the left child.

Given the output S of this traversal, recover the tree and return its root.

Example 1:

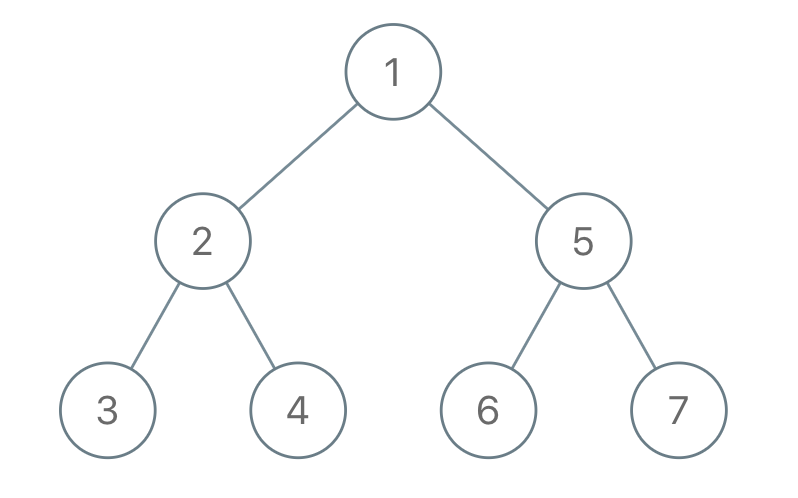
Input: "1-2--3--4-5--6--7"
Output: [1,2,5,3,4,6,7]

Example 2:

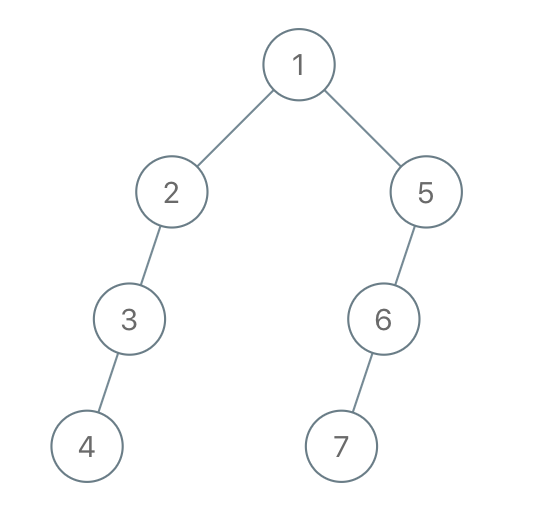
Input: "1-2--3---4-5--6---7"
Output: [1,2,5,3,null,6,null,4,null,7]

Example 3:

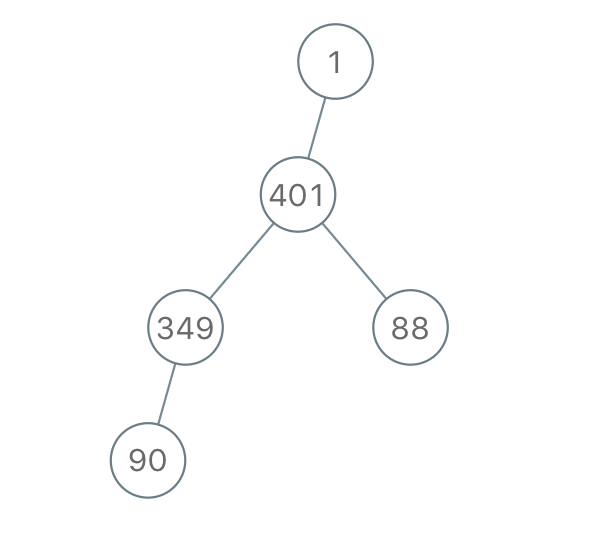
Input: "1-401--349---90--88"
Output: [1,401,null,349,88,90]

Note:

• The number of nodes in the original tree is between 1 and 1000.
• Each node will have a value between 1 and 10^9.

Solution

递归好用

Code

class Solution(object):
    def recoverFromPreorder(self, S):
        """
        :type S: str
        :rtype: TreeNode
        """
        def build_tree(nodes, depths):
            if len(nodes) == 0:
                return None
            if len(nodes) == 1:
                return TreeNode(nodes[0])
            root = TreeNode(nodes[0])
            sub_depth = depths[1]
            # if only left child
            if depths.count(sub_depth) == 1:
                root.left = build_tree(nodes[1:], depths[1:])
            else:
                right_idx = depths[2:].index(sub_depth) + 2
                root.left = build_tree(nodes[1:right_idx], depths[1:right_idx])
                root.right = build_tree(nodes[right_idx:], depths[right_idx:])
            return root
            
        pre_dash_count = 0
        cur_num = 0
        idx = 0
        length = len(S)
        nodes = []
        depths = []
        
        while idx < len(S):
            if S[idx].isdigit():
                while idx < length and S[idx].isdigit():
                    cur_num = cur_num*10 + int(S[idx])
                    idx += 1
                nodes.append(cur_num)
                depths.append(pre_dash_count)
                cur_num = 0
                pre_dash_count = 0
            else:
                while idx < length and S[idx]=='-':
                    pre_dash_count += 1
                    idx += 1
        print(nodes)    # [1, 2, 3, 4, 5, 6, 7]
        print(depths)   # [0, 1, 2, 2, 1, 2, 2]
        
        return build_tree(nodes, depths)