|
| 1 | +Hello Everyone, |
| 2 | + |
| 3 | +Learned some hard problem solving technique using Binary Index Tree(BIT) , wanted to share . Feel free to point any mistake and add more problems to this thread. |
| 4 | + |
| 5 | +**Pre-requiste** |
| 6 | +You can learn about BIT from wikipedia or these resource |
| 7 | +https://www.youtube.com/watch?v=v_wj_mOAlig |
| 8 | +https://www.youtube.com/watch?v=uSFzHCZ4E-8 |
| 9 | + |
| 10 | +You should also be aware of how to do combination of range update and point queries(check wikipedia) or |
| 11 | +https://leetcode.com/discuss/general-discussion/1093346/introduction-to-fenwick-treebinary-indexed-treebit |
| 12 | + |
| 13 | +**Warm-up Problems:** |
| 14 | +After reading about basic of BIT, you must solve these 2 problems to get hands dirty on BIT. |
| 15 | +Solving these gives confidence in BIT and they are easy but important problems. |
| 16 | +Make sure to use long long. |
| 17 | + |
| 18 | +https://www.spoj.com/problems/FENTREE/ |
| 19 | +https://www.spoj.com/problems/UPDATEIT/ |
| 20 | + |
| 21 | +**Hard Problems**: |
| 22 | +Real fun starts here. |
| 23 | +- Fisrt familirize with what is lower_bound & upper_bound. |
| 24 | +1.lower_bound first iterator of value <= |
| 25 | +2.upper_bound return value > |
| 26 | +3.in case in lower_bound you need last index <= (GFG problem requires that) just do upper_bound -1. in this diagram you get index 6 then. |
| 27 | + |
| 28 | + |
| 29 | + |
| 30 | + |
| 31 | +- Whether to iterate from begining or end of vector. |
| 32 | +Mostly you iterate from begining unless problem ( like LC 315) asked something specific. |
| 33 | + |
| 34 | +**Template:** |
| 35 | +1. Copy the input vector into another vector and sort it. Why we need another sorted vector is an important concept to understand here since this is used in all problem. |
| 36 | + Basically in Step 4 we iterate the input array (not the sorted array) and we find its position in sorted array and then see how many element before or after (depend on problem) |
| 37 | + occured and then sum it up. Will explain in detail in the problem. |
| 38 | +2. Setup BIT array of 1+n , where n is array size. |
| 39 | +3. Iterate from begin/ end. |
| 40 | +4. See what the problme is asking for and acording use lower/upper bound We want everything less than current |
| 41 | +5. Update the frequency of this current element in BIT array. |
| 42 | + |
| 43 | +Lets see this template working in this problem. |
| 44 | +[LC 315: Smaller Number than Self](https://leetcode.com/problems/count-of-smaller-numbers-after-self/) |
| 45 | +Step 1 & 2 is standard. |
| 46 | +Step 3 : This question asked every element smaller on its right side, so start from end. |
| 47 | +Step 4: Problem is asking for less than current element so lower_bound is needed. |
| 48 | + Since BIT works on 1 index, increment index by 1. |
| 49 | + Now we want everything less than current value so sum(index -1). |
| 50 | +Step 5: Increment index by 1. |
| 51 | + |
| 52 | +Step 4 & 5 in detail |
| 53 | +A = [5,2,6,1] |
| 54 | +Sorted_A = [1, 2, 5, 6] |
| 55 | +BIT = [0, 0, 0, 0, 0] |
| 56 | + |
| 57 | +loop from end |
| 58 | +i = 3 |
| 59 | + nums[i] = 1 |
| 60 | + its position in Sorted_A is 0 (lower_bound of 1 is 1 itself) |
| 61 | + BIT works on 1 index so index is 1. |
| 62 | + now we want everything less than 1 so sum(0) which gives 0 and we know nothing is less than 1 on right side so res[3] = 0 |
| 63 | + update idx=1 in BIT array , we are trying to communicate to all higher index that a smaller number (1) is available. |
| 64 | + This is a key part in understand which direction to update and which direction to sum, if you see 493 the process(sum and update) is exact reverse. |
| 65 | + so BIT = [0, 1, 1, 0, 1] (1st , 2nd and 4th index is incremented by 1) |
| 66 | +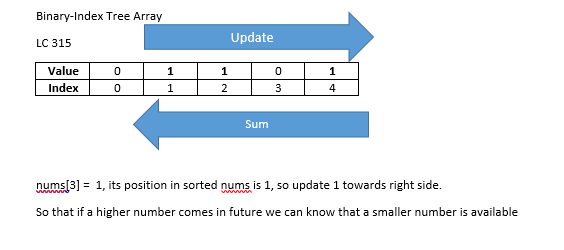 |
| 67 | + |
| 68 | +i=2 |
| 69 | + nums[i] = 6 |
| 70 | + position in sorted_A is 3 |
| 71 | + +1 for BIT index = 4 |
| 72 | + we want all less than this index so sum(3) |
| 73 | + now since 1 occured in previous iteration and it has updated BIT array so sum(3) gives 1, res[2] = 1 |
| 74 | + after update(4) we get BIT = [0, 1, 1, 0, 2] |
| 75 | +``` |
| 76 | +class Solution { |
| 77 | + vector<int> BIT; |
| 78 | + int sum (int idx){ |
| 79 | + int ret =0; |
| 80 | + for(; idx > 0; idx -= (idx & -idx)) |
| 81 | + ret += BIT[idx]; |
| 82 | + return ret; |
| 83 | + } |
| 84 | + void update(int idx){ |
| 85 | + for(; idx < BIT.size(); idx += (idx & -idx)) |
| 86 | + BIT[idx]++; |
| 87 | + } |
| 88 | +public: |
| 89 | + vector<int> countSmaller(vector<int>& nums) { |
| 90 | + int n = nums.size(); |
| 91 | + vector<int> sorted(nums); |
| 92 | + sort(sorted.begin(), sorted.end()); // Step 1 |
| 93 | + BIT.resize(1+n); // Step 2 |
| 94 | + vector<int> ans(nums.size()); |
| 95 | + for(int i =n-1; i>=0; --i){ |
| 96 | + int idx = lower_bound(sorted.begin(), sorted.end(), nums[i]) - sorted.begin(); |
| 97 | + ++idx;// since BIT starts with 1 |
| 98 | + ans[i] = sum(idx-1); |
| 99 | + update(idx); |
| 100 | + } |
| 101 | + return ans; |
| 102 | + } |
| 103 | +``` |
| 104 | + |
| 105 | +[LC 493: Reverse Pair](https://leetcode.com/problems/reverse-pairs/) |
| 106 | +Exactly same as above but one key difference |
| 107 | +Here if we get smaller number , we need to get the count of all the bigger number (2 * x - 1 ) appeared in past iteration . |
| 108 | +Now since the smaller number index would be smaller, all the bigger number has to tell to the left of it . that means update should happen toward left. |
| 109 | +``` |
| 110 | +class Solution { |
| 111 | + int n; |
| 112 | + vector<int> BIT; |
| 113 | + int sum(int i){ |
| 114 | + int ret = 0; |
| 115 | + for(; i < BIT.size(); i += (i & -i)) |
| 116 | + ret += BIT[i]; |
| 117 | + return ret; |
| 118 | + } |
| 119 | + void update(int i){ |
| 120 | + for(; i >0; i -= (i & -i)) |
| 121 | + BIT[i]++; |
| 122 | + } |
| 123 | +public: |
| 124 | + int reversePairs(vector<int>& nums) { |
| 125 | + n = nums.size(); |
| 126 | + BIT.resize(1+n); |
| 127 | + vector<int> sorted_nums(nums); |
| 128 | + sort(sorted_nums.begin(), sorted_nums.end()); |
| 129 | + int ans = 0; |
| 130 | + for(int i =0; i < n; ++i){ |
| 131 | + int idx = lower_bound(sorted_nums.begin(), sorted_nums.end() , (long)2*nums[i] + 1) - sorted_nums.begin(); |
| 132 | + |
| 133 | + ++idx; |
| 134 | + ans += sum(idx); |
| 135 | + idx = lower_bound(sorted_nums.begin(), sorted_nums.end(), nums[i]) - sorted_nums.begin(); |
| 136 | + ++idx; |
| 137 | + update(idx); |
| 138 | + } |
| 139 | + return ans; |
| 140 | + } |
| 141 | +}; |
| 142 | +``` |
| 143 | + |
| 144 | +Try solving this problem too, same as above, except lower/upper bound difference. |
| 145 | +https://www.spoj.com/problems/INVCNT/ |
| 146 | + |
| 147 | +**BIT using Prefix Sum** |
| 148 | + |
| 149 | +Key difference is instead of number , we are asked sub-array whose sum lies in certain range. |
| 150 | +Basically the problem involved sub-array instead of array element. |
| 151 | + |
| 152 | +When problem asked for subarray sums, one standard approach come to mind is prefix sum. |
| 153 | +1. Generate prefix sum |
| 154 | +2. Generate sorted prefix_sum |
| 155 | +These two will replace the nums & sorted_nums in template. |
| 156 | +Also assign a unique rank or number to each of the psum, why are we doing it, because we are using this unique number to update the BIT. |
| 157 | +remember that psum can be -ve and BIT works on +ve indices |
| 158 | +you have 2 option , |
| 159 | +1. either make all the psum +ve |
| 160 | +2. or assign a unique rank to each psum and then use this unique rank to update BIT. |
| 161 | +For more details I added another post https://leetcode.com/problems/count-of-smaller-numbers-after-self/discuss/1547068/binary-index-tree-in-2-different-ways |
| 162 | + |
| 163 | +[327. Count of Range Sum](https://leetcode.com/problems/count-of-range-sum/) |
| 164 | + |
| 165 | + [-2,5,-1], lower = -2, upper = 2 |
| 166 | + Suppose psum[i] is 7 , we are looking if any previous psum lies in range [5, 9] |
| 167 | + which means [psum[i]-upper , psum[i]-lower] |
| 168 | + so look for this psum in sorted_psum and then do the sum(higher)-sum(lower) |
| 169 | + finally update(rank(psum[i])) ; remember we are dealing BIT index on rank of psum not the psum itself as psum cna be -ve. |
| 170 | +``` |
| 171 | +class Solution { |
| 172 | + vector<int> BIT; |
| 173 | + int n; |
| 174 | + void update(int i){ |
| 175 | + for(; i < BIT.size(); i += (i & -i)) |
| 176 | + BIT[i]++; |
| 177 | + } |
| 178 | + int sum(int i){ |
| 179 | + int ret =0; |
| 180 | + for(; i > 0; i -= (i& -i)) |
| 181 | + ret += BIT[i]; |
| 182 | + return ret; |
| 183 | + } |
| 184 | +public: |
| 185 | + int countRangeSum(vector<int>& nums, int lower, int upper) { |
| 186 | + n = nums.size(); |
| 187 | + vector<long> psum(1+n, 0); |
| 188 | + for(int i =0; i <n; ++i) |
| 189 | + psum[i+1] = psum[i] + nums[i]; |
| 190 | + vector<long> sorted_psum(psum); |
| 191 | + sort(sorted_psum.begin(), sorted_psum.end()); |
| 192 | + // Give a unique id to each psum |
| 193 | + unordered_map<int, int> rank; |
| 194 | + for(int i =0; i <= n ; ++i) |
| 195 | + rank[sorted_psum[i]] = 1+i; |
| 196 | + BIT.resize(2+n, 0);// WHy 2 because 1 for BIT index starts with 1 index |
| 197 | + // 2nd one is because our psum array has a 0 sum also |
| 198 | + // Why we added 0 because psum -lower or upper could be 0. |
| 199 | + int ans =0; |
| 200 | + for(int i =0; i <= n ; ++i){ |
| 201 | + long up = psum[i] - lower; |
| 202 | + long lo = psum[i] - upper; |
| 203 | + // Now check in sorted psum array |
| 204 | + int lower_idx = lower_bound(sorted_psum.begin(), sorted_psum.end(), lo)-sorted_psum.begin(); |
| 205 | + int higher_idx = upper_bound(sorted_psum.begin(), sorted_psum.end(), up)-sorted_psum.begin(); |
| 206 | + ans += sum(higher_idx) - sum (lower_idx); |
| 207 | + update(rank[psum[i]]); |
| 208 | + } |
| 209 | + return ans; |
| 210 | + } |
| 211 | +}; |
| 212 | +``` |
| 213 | + |
| 214 | +[GFG Count of substrings in a Binary String that contains more 1s than 0s](https://www.geeksforgeeks.org/count-of-substrings-in-a-binary-string-that-contains-more-1s-than-0s/) |
| 215 | +The page suggest using merge sort but I did using BIT with same time complexity. Try BIT way. |
| 216 | +Will add more problem to this list. |
| 217 | + |
| 218 | +**End Note:** |
| 219 | +- Make sure you can now write bug free update and sum routine , its fairly easy after some practice. |
| 220 | +- Notice what problem is asking and apply the template. |
| 221 | +- If problem involved prefix sum, use rank method and use that array instead. |
| 222 | +- Think where to start iterarting from. |
| 223 | +- lower_bound/upper_bound what to use |
| 224 | +- In general, it problem is asking for some kind of count in array ranges, think if BIT can be applied in some way. |
| 225 | + |
0 commit comments