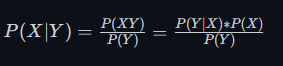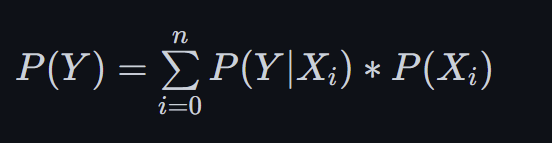贝叶斯要解决的问题: 如何计算逆向概率
正向概率:已知袋子里有 M 个黑球, N 个白球,摸一个球摸出黑球的概率是多大?
逆向概率:一个未知的袋子里有一些黑球和白球,随机摸出一个或者好几个球,观察摸出的球可以对袋子里的黑球白球的比例做出什么样的推测?
举一个更形象的例子:
已知学校中的60%的人是男生,40%的人是女生,其中男生总是穿着长裤,女生则一半穿长裤,一半穿裙子
正向概率:随机选择一个男生或者女生,他/她穿长裤/裙子的概率是多少?
逆向概率:迎面走来一个穿着长裤的人,不能确定ta的性别,你能推断出ta是男生/女生的概率是多少?
条件概率的公式为 P(X|Y),表示在已知 Y 情况下 X 发生的概率
所以对于正向概率,即我们已知男生女生,只需要根据题目中的概率直接就可以计算穿长裤和穿裙子的概率:
- P(穿长裤|男生) = 1
- P(穿裙子|男生) = 0
- P(穿长裤|女生) = 0.5
- P(穿裙子|女生) = 0.5
对于逆向概率,我们想求的是 P(男生|穿长裤) 和 P(女生|穿长裤),这并不好直接计算
贝叶斯公式有一个推导式: P(X|Y) = P(XY)/P(Y),所以这个问题可以转化为 P(男生并且穿长裤)/P(穿长裤) 和 P(女生并且穿长裤)/P(穿长裤)
这时分子分母都是可以计算的式子. 假设总人数 N ,穿长裤的人数为 N*P(男)*1+N*P(女生)*0.5,男生并且穿长裤的人数为 N*P(男)*1,女生并且穿长裤的人数为N*P(女)*0.5,上下相除 N 被约掉
我们可以将分子的 P(XY)分解, 等价于 P(Y|X)*P(X),具体来说就是P(男生并且穿长裤) = P(穿长裤|男生)*P(男生)
所以我们在求逆向概率的时候得到了一个神奇的变换:
贝叶斯公式就是在计算逆向概率的时候我们遇到一个不好直接求的条件概率,但是如果我们便于计算其反过来的条件概率,变换之后就很容易计算了
计算中我们注意到一个问题,就是这个情况下只有男生女生两类,也就是说穿长裤的不是男生就是女生,所以P(穿长裤) = P(穿长裤|男生)*P(男生) + P(穿长裤|女生)*P(女生),分解一个大的概率P(X),它可以由几种情况组成,我们可以写成公式
接下来考虑一个更为复杂也更为实际的情况.如何判断一封邮件是否是垃圾邮件?也就是说我们需要求出 P(垃圾邮件|邮件内容),很显然这个概率明显不好求. 我们使用贝叶斯公式
P(垃圾邮件|邮件内容) = P(垃圾邮件和邮件内容) / P(邮件内容) = P(邮件内容|垃圾邮件) * P(垃圾邮件) / P(邮件内容)其中最后的 P(邮件内容) 对结果并没有影响,因为P(正常邮件|邮件内容)的分母也有此项,可以认为是一个常数,也就是说 P(垃圾邮件|邮件内容) 正相关于 P(邮件内容|垃圾邮件) * P(垃圾邮件)
所以现在我们将判断一封邮件是否是垃圾邮件这个问题的概率转化为 P(垃圾邮件) * P(邮件内容|垃圾邮件),那么怎么求求这两个的概率呢?
这一部分的概率称为先验概率,先验概率prior probability是指根据以往经验和分析得到的概率,比如P(硬币正面朝上)=0.5,可以认为是根据大数定律,频率趋近于概率,也就是说我们找足够多的数据样本(10万封邮件或者更多),那么其中垃圾邮件出现的频率(6万次)就可以认为是P(垃圾邮件) = 6/10 = 0.6,这一部分的概率是根据一个巨大先验集(训练集)来确定的
另一部分就是垃圾邮件中邮件内容出现的概率了,显然不可能完整的计算整封邮件内容,考虑到一封邮件是由词 ABCD... 组成,这个概率可以被拆开,
正常情况下一封邮件的每一个词之间都是有前后文关联的,"我喜欢打篮球"和"喜欢打蓝我球"显然是不同的语义,这个概率应该被写作
P(邮件内容|垃圾邮件) = P(A|垃圾邮件) * P(B|A,垃圾邮件) * P(C|B,A,垃圾邮件) ....也就是说每一个词出现的概率都需要计算前面的词已经出现的过的概率,这个计算量是巨大的.朴素贝叶斯的思想就是体现在这里,假设每个特征之间是相互独立的. "我喜欢打篮球"和"喜欢打蓝我球",只要是这五个字的排列组合我都认为是同一种情况没有区别,这大大减少了计算量
P(邮件内容|垃圾邮件) = P(A|垃圾邮件) * P(B|垃圾邮件) * P(C|垃圾邮件) ...也就是我们只需要统计出先验集(训练集)的垃圾邮件中邮件内容的每个词出现的概率就可以了,这时会产生一个问题,如果这个词没有出现过那该怎么做呢?
对于一个从未见过的词,在训练集中没有对应的概率值, P(X|垃圾邮件) = 0 ? ,这显然是不合适的,因为我们计算概率 P(邮件内容|垃圾邮件)的时候需要把每个词的概率相乘.某一项为0显然是我们不希望看到的结果.
而这个错误的造成是由于训练量不足,会令分类器质量大大降低。为了解决这个问题,我们引入 Laplace校准(拉普拉斯平滑),它的思想非常简单,就是对每个类别下所有划分的计数加1,这样如果训练样本集数量充分大时,并不会对结果产生影响,并且解决了上述频率为0的尴尬局面
举个例子: 如果垃圾邮件中有 2个"售",3个"买",...,现在的词是"购",在原数据集中并没有出现,那么对于垃圾邮件中每个词数量加一,变为3个"售",4个"买",1个"购"....,这样每个类都加了一个当数据集足够大时基本没什么影响.
在垃圾邮件分类中,比较常见的公共数据集有Apache SpamAssassin和TREC Spam Corpus和CEAS等.
不过这些数据集的处理较为复杂,因为原始的邮件数据格式不一致,语言不一致,数据量又太大了,处理起来很慢效果也不是很理想,最后选择用两个教学常用的数据集
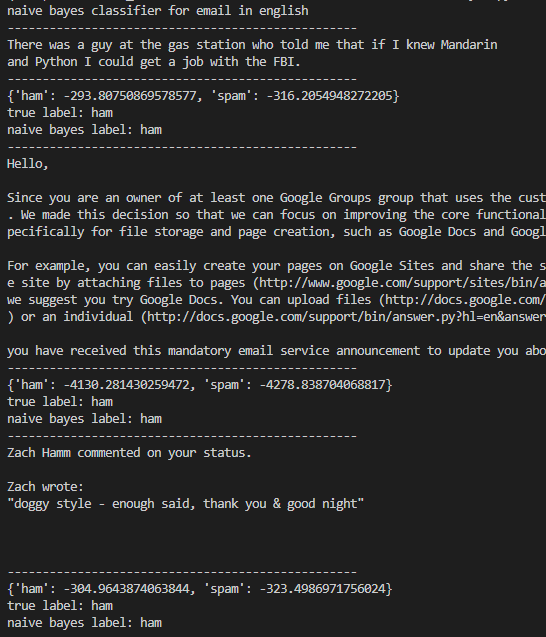
- email: 已经处理好的邮件分类,判断垃圾邮件还是正常邮件
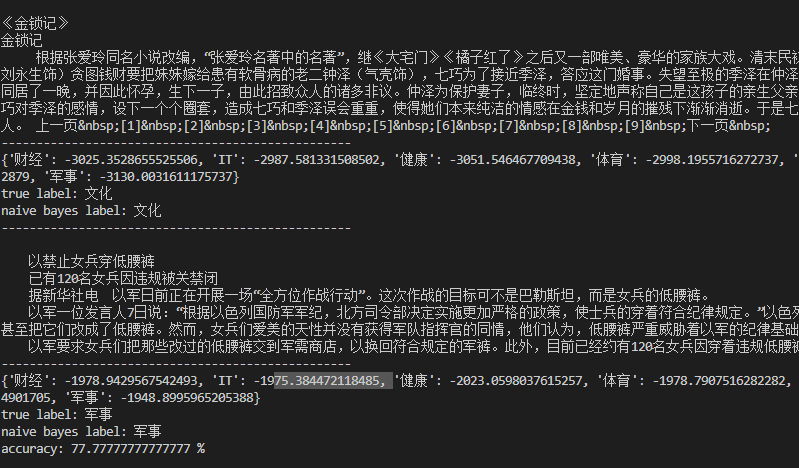
- SougouC: 搜狗新闻数据集,判断属于哪一类
-
使用email数据集
python main.py --email
-
使用搜狗数据集
python main.py --sougou
素贝叶斯分类的优缺点
-
优点:
- 算法逻辑简单,易于实现
- 分类过程中时空开销小
-
缺点:
- 理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好.
- 而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进.
- 首先先验集并不是从一个大样本中筛选出来的,所以导致每一个类的初始先验概率相同.事实上垃圾邮件的数量会多于正常邮件,搜狗中也并不是这九个类的先验概率相同,这显然是不合理的.
- 其次如果真的完全按照朴素贝叶斯公式来计算也是存在问题的,因为朴素贝叶斯公式是要求各个特征的概率值相乘,多个(0~1)且接近0的小数相乘很容易造成python的下溢出,导致概率归0.
-
解决方法为利用
math.log函数的性质,单调递增,内部的乘积可以转化为外部的加法$$log(a*b*c) = log(a)+log(b)+log(c)$$ 把概率的累乘变为多个log的累加,且由于单调递增的性质不会对结果造成影响
-