-
Modern day machine learning requires lots of labeled data. But often times it's challenging and/or expensive to obtain large amounts of human-labeled data. Is there a way we could ask machines to automatically learn a model which can generate good visual representations without a labeled dataset? Yes, enter self-supervised learning!
-
Self-supervised learning (SSL) allows models to automatically learn a "good" representation space using the data in a given dataset without the need for their labels. Specifically, if our dataset were a bunch of images, then self-supervised learning allows a model to learn and generate a "good" representation vector for images.
-
The reason SSL methods have seen a surge in popularity is because the learnt model continues to perform well on other datasets as well i.e. new datasets on which the model was not trained on!
- A "good" representation vector needs to capture the important features of the image as it relates to the rest of the dataset. This means that images in the dataset representing semantically similar entities should have similar representation vectors, and different images in the dataset should have different representation vectors. For example, two images of an apple should have similar representation vectors, while an image of an apple and an image of a banana should have different representation vectors.
-
Recently, SimCLR introduces a new architecture which uses contrastive learning to learn good visual representations. Contrastive learning aims to learn similar representations for similar images and different representations for different images. As we will see in this notebook, this simple idea allows us to train a surprisingly good model without using any labels.
-
Specifically, for each image in the dataset, SimCLR generates two differently augmented views of that image, called a positive pair. Then, the model is encouraged to generate similar representation vectors for this pair of images. See below for an illustration of the architecture .
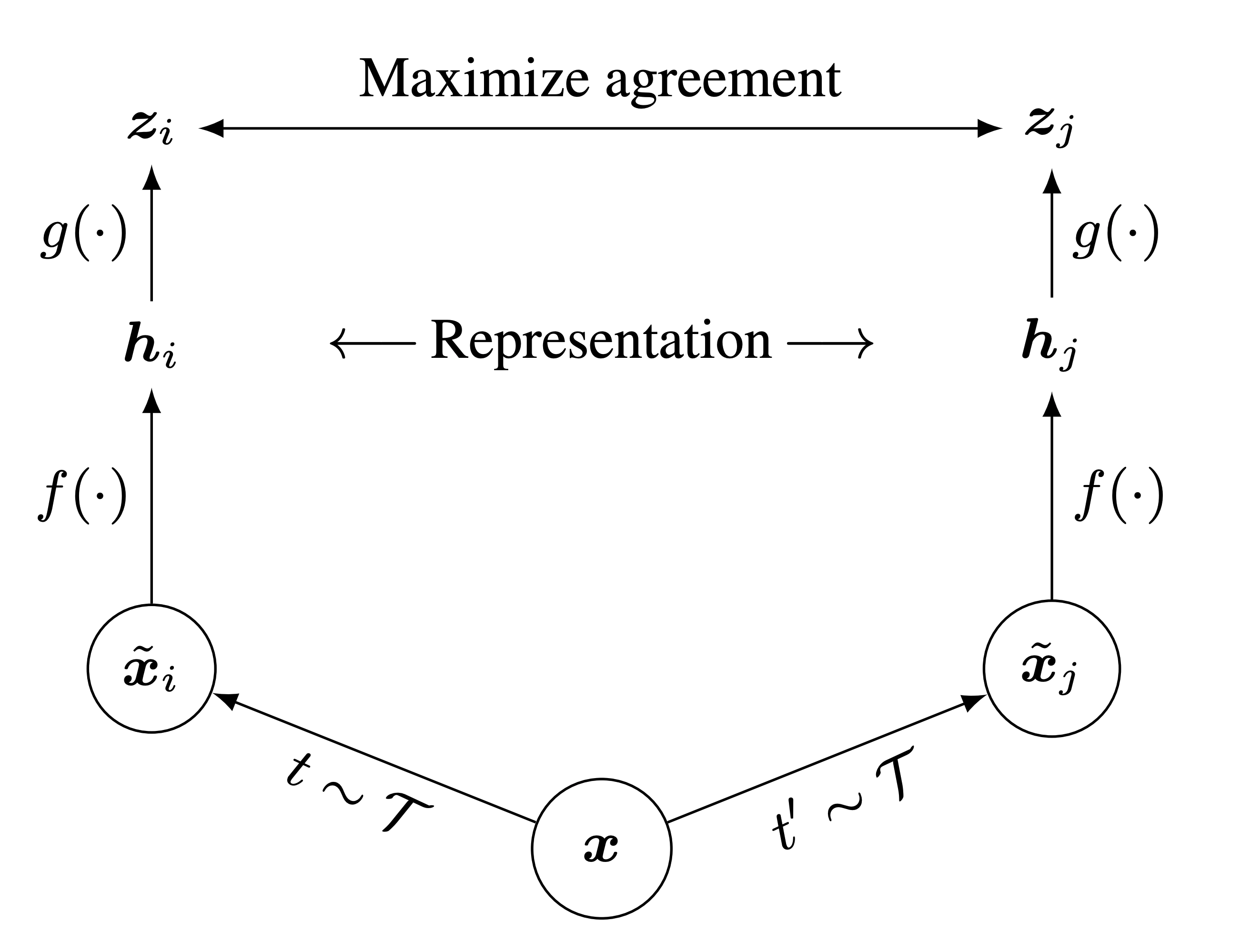
-
Given an image x, SimCLR uses two different data augmentation schemes t and t' to generate the positive pair of images x
i and xj . f is a basic encoder net that extracts representation vectors from the augmented data samples, which yields hi and hj , respectively. Finally, a small neural network projection head g maps the representation vectors to the space where the contrastive loss is applied. The goal of the contrastive loss is to maximize agreement between the final vectors zi=g(hi) and zj=g(hj) . We will discuss the contrastive loss in more detail later, and we will implement it. -
After training is completed, we throw away the projection head g and only use f and the representation h to perform downstream tasks, such as classification. We will finetune a layer on top of a trained SimCLR model for a classification task and compare its performance with a baseline model (without self-supervised learning).
-
A mini-batch of N training images yields a total of 2N data-augmented examples. For each positive pair (i,j) of augmented examples, the contrastive loss function aims to maximize the agreement of vectors zi and zj . Specifically, the loss is the normalized temperature-scaled cross entropy loss and aims to maximize the agreement of zi and zj relative to all other augmented examples in the batch:
-
l(i,j)=−logexp(sim(zi,zj)/τ)∑2Nk=11k≠iexp(sim(zi,zk)/τ)
-
where 1∈{0,1} is an indicator function that outputs 1 if k≠i and 0 otherwise. τ is a temperature parameter that determines how fast the exponentials increase.
-
sim(zi,zj)=zi⋅zj||zi||||zj|| is the (normalized) dot product between vectors zi and zj. The higher the similarity between zi and zj, the larger the dot product is, and the larger the numerator becomes. The denominator normalizes the value by summing across zi and all other augmented examples k in the batch. The range of the normalized value is (0,1), where a high score close to 1 corresponds to a high similarity between the positive pair (i,j) and low similarity between i and other augmented examples k in the batch. The negative log then maps the range (0,1) to the loss values (inf,0).
-
The total loss is computed across all positive pairs (i,j) in the batch. Let z=[z1,z2,...,z2N] include all the augmented examples in the batch, where z1...zN are outputs of the left branch, and zN+1...z2N are outputs of the right branch. Thus, the positive pairs are (zk,zk+N) for ∀k∈[1,N].
-
Then, the total loss L is: $$ L = \frac{1}{2N} \sum_{k=1}^N [ ; l(k, ;k+N) + l(k+N, ;k);] $$
-
NOTE: this equation is slightly different from the one in the paper. We've rearranged the ordering of the positive pairs in the batch, so the indices are different. The rearrangement makes it easier to implement the code in vectorized form.
-
We'll walk through the steps of implementing the loss function in vectorized form. Implement the functions sim, simclr_loss_naive in resources/simclr/contrastive_loss.py. Test the code by running the sanity checks below.
-
Now it's time to put the representation vectors to the test!
-
We remove the projection head from the SimCLR model and slap on a linear layer to finetune for a simple classification task. All layers before the linear layer are frozen, and only the weights in the final linear layer are trained. We compare the performance of the SimCLR + finetuning model against a baseline model, where no self-supervised learning is done beforehand, and all weights in the model are trained. You will get to see for yourself the power of self-supervised learning and how the learned representation vectors improve downstream task performance.
- First, we take a look at the baseline model. We'll remove the projection head from the SimCLR model and slap on a linear layer to finetune for a simple classification task. No self-supervised learning is done beforehand, and all weights in the model are trained.
- See how much improvement we get with self-supervised learning.We pretrain the SimCLR model using the simclr loss we wrote, remove the projection head from the SimCLR model, and use a linear layer to finetune for a simple classification task.